Multi-agent Reinforcement Learning

Our recent focus has been on finding Nash equilibria in Markov games. Two representative papers include computing Nash Equilibria in Adversarial Team Markov Games. and in Markov Potential Games. Other works include analysis of natural policy gradient in multi-agent settings.

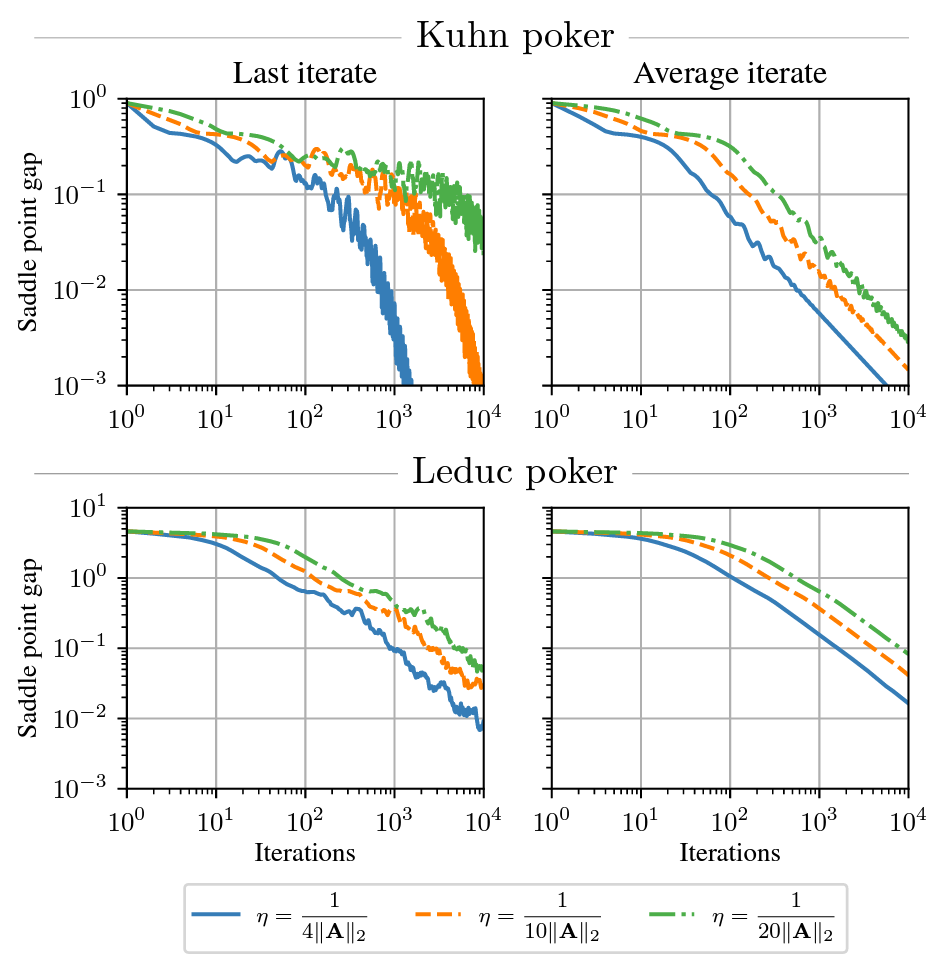
Learning in Games

The PI and the group is actively working on learning in games. Papers include results on last iterate convergence using optimism in zero-sum games and beyond (like potential games). Other works include proving cycling or even chaotic behavior of the learning dynamics, the analysis of average performance of learning in games and stability analysis in evolutionary dynamics.

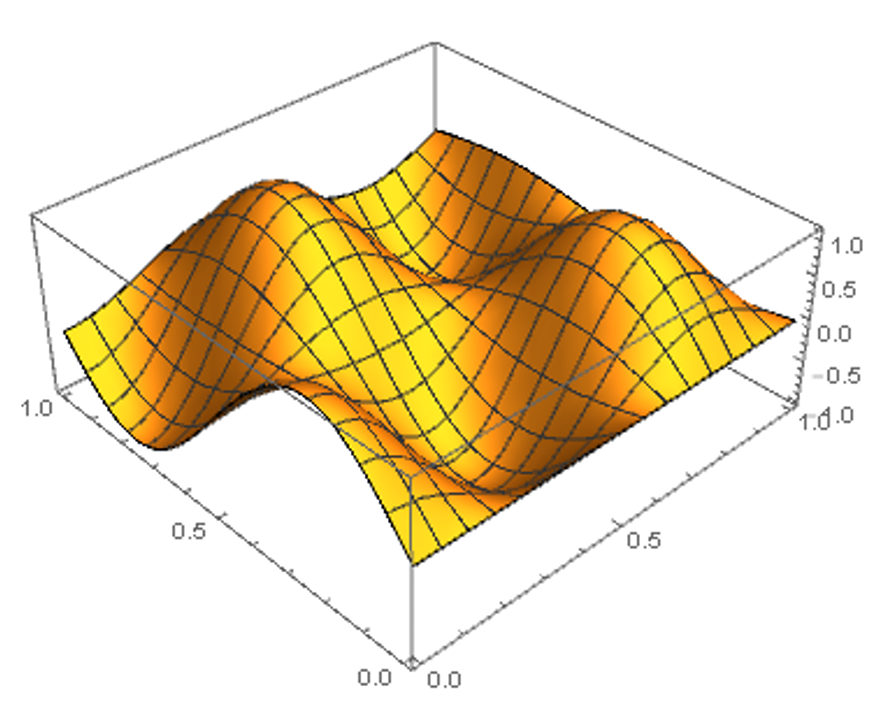
Non-convex and min-max optimization

Inspired by the success of Stochastic Gradient Descent in training neural networks, the group has done works on non-convex optimization. Using techniques from dynamical systems, we are able to show that Gradient Descent and other first order methods with constant stepsize avoid strict saddle points. We extend these results to multiplicative weights update (polytope constraints) and time varying stepsizes. Inpired by the success of Generative Adversarial Networks, the group has worked on min-max optimization for non-convex non-concave landscapes, characterising the limit points of first-order methods.

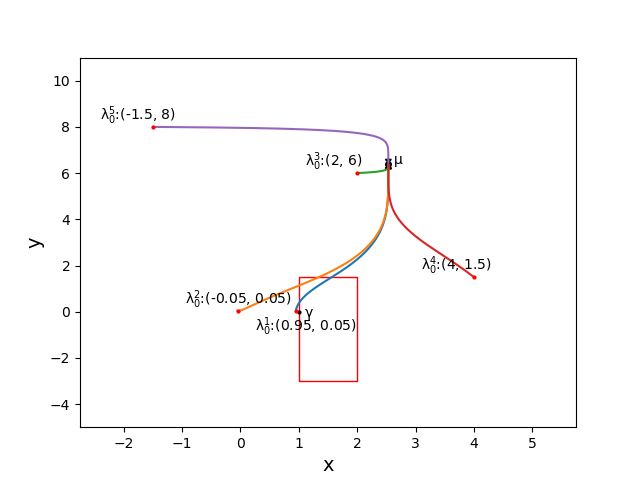
Probability and Statistics

The group has works related to proper learning in Graphical models with applications to learning from dependent data (see also this paper for a setting using hypergraphs), structural learning from truncated data, learning mixtures from truncated data. Other works are about bounding the mixing time in Markov Chains (see also follow-up paper)

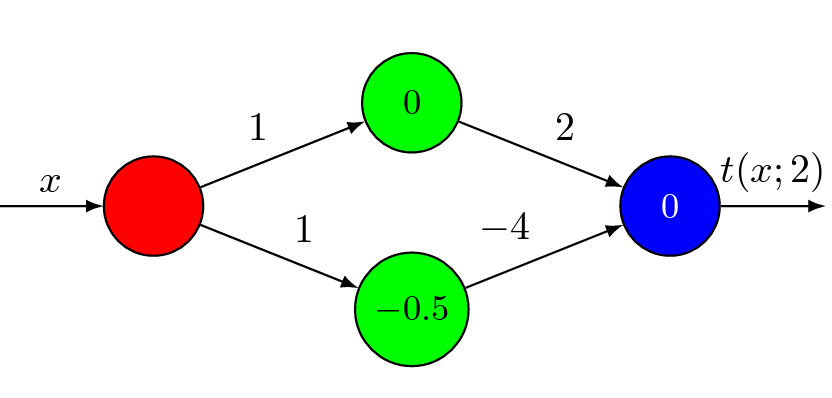
Deep Learning Theory

Our group has focused on the problem of expressivity of Neural Networks. Using techniques from Dynamical systems, we are able to prove tradeoffs between the depth and the width in feedforward Neural Networks. Here is also a follow-up paper that strenghtens the results.

Our team includes 3 PhD students, multiple undergrads and external collaborators. Meet our team